在微积分的学习中，我们常常需要求各种函数的导数，而函数y = tan(x)是一种常见的三角函数。下面将详细解释tan函数的导数及其推导过程。
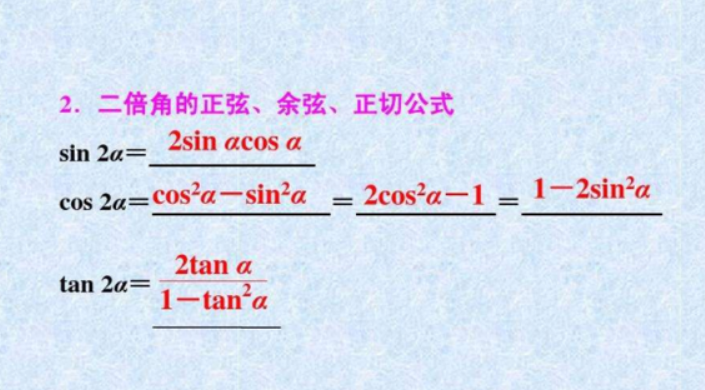
一、tan函数的定义和特点
tan函数是正切函数的简称，它表示一个角（弧度）的正切值。tan函数的定义域为所有实数，值域为正负无穷。在单位圆上，tan函数的值等于相应角的对边长度与邻边长度的比值。在数学中，它有如下基本性质：
1. tan(0) = 0， tan(π) = 0， tan(2π) = 0；
2. tan(π/4) = 1， tan(-π/4) = -1；
3. tan(π/2) = 正无穷， tan(-π/2) = 负无穷。
二、tan函数的图像及相关概念
通过绘制函数y = tan(x)的图像，我们可以得知以下结论：
1. tan函数在每个周期内都是周期性函数，其周期为π；
2. 当x = kπ + π/2（k为整数）时，tan函数的值取正无穷；
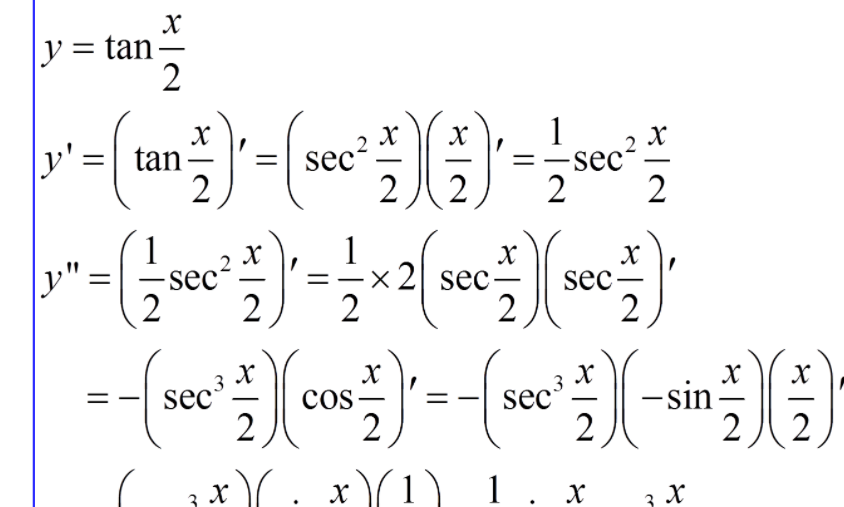
3. 当x = kπ（k为整数）时，tan函数的值为0；
4. 当x = kπ - π/2（k为整数）时，tan函数的值取负无穷。
三、tan函数的导数公式及推导过程
要求tan函数的导数，我们需要找到tan函数的导数公式并进行推导。
1. 导数公式：
tan函数的导数公式是：(d/dx)tan(x) = sec^2(x)。
2. 推导过程：
根据导数的定义及函数的极限，我们可以推导出tan函数的导数公式。
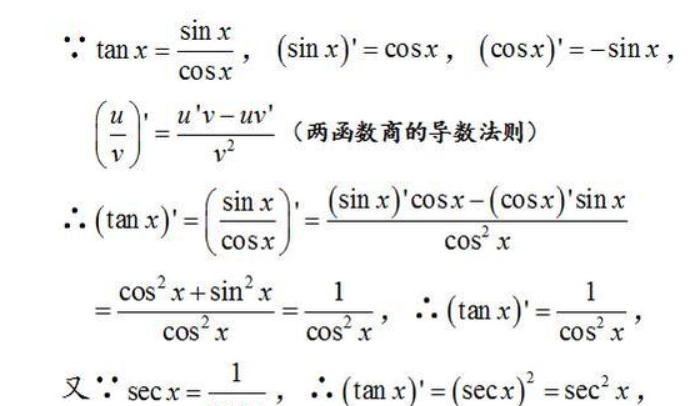
设y = tan(x)，则tan函数的导数可以表示为dy/dx。
根据极限定义，dy/dx的定义如下：
dy/dx = lim（h->0）[tan(x + h) - tan(x)] / h
对极限式中的差商进行处理，化简为：
dy/dx = lim（h->0）[(sin(x + h) / cos(x + h)) - (sin(x) / cos(x))] / h
再整理一下分子的式子：
dy/dx = lim（h->0）[sin(x + h)cos(x) - sin(x)cos(x + h)] / hcos(x)cos(x + h)
利用正弦和余弦的和差化积公式，将分子整理得更简洁：
dy/dx = lim（h->0）[(sin(x)cos(h) + sin(h)cos(x))cos(x) - sin(x)[cos(x)cos(h) - sin(x)sin(h)]] / hcos(x)cos(x + h)
进行进一步的化简，得到：
dy/dx = lim（h->0）[sin(x)cos(h) + sin(h)cos(x) - sin(x)cos(x)cos(h) + sin^2(x)sin(h)] / hcos(x)cos(x + h)
继续化简，得到：
dy/dx = lim（h->0）[(sin(x) + sin(h))cos(x) + sin(x)(1 - cos^2(h)) / hcos(x)cos(x + h)
由三角函数的极限性质，得到：
dy/dx = sin(x)cos(x) / cos^2(x)
利用三角函数的平方和差化积公式，将分子和分母整理得更简洁：
dy/dx = sin(x) / cos(x) =tan(x)
总结：tan函数的导数等于它本身，即：
(d/dx)tan(x) = sec^2(x)。
四、结论
通过以上推导，我们得到了tan函数的导数公式，即(sec^2(x))。这意味着，tan函数的导数等于它的平方函数sec^2(x)。这个结论对于解决具体的数学问题和实际应用有着重要的意义。
