导数是数学中重要的概念之一，它描述了函数在某一点附近的变化率。在三角函数中，tanx是一种常见的函数，其导数也具有一定的特点。下面将详细讨论tanx的导数。
一、tanx的定义及性质
tanx是三角函数中的一种，定义为对边与邻边的比值，即tanx=opposite/adjacent。tanx的定义域是所有实数，但在一些特定的点上它的值是无穷大的。tanx是一个周期函数，周期为π，即tan(x+π) = tanx。
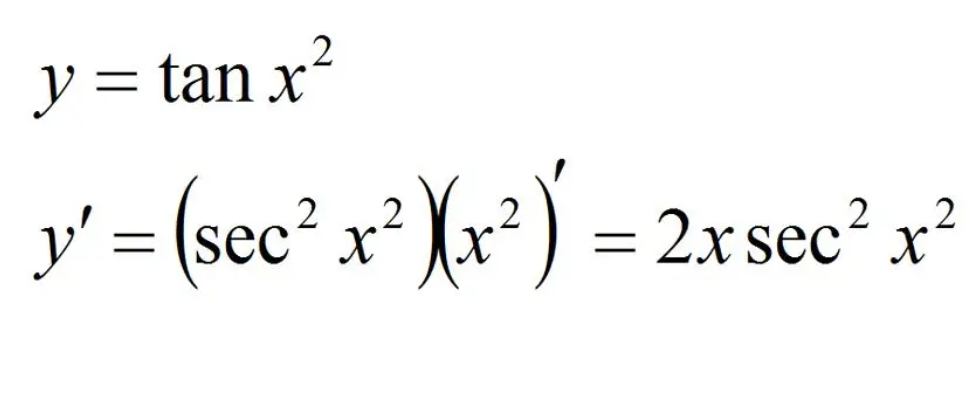
二、使用极限计算tanx的导数
要计算tanx的导数，可以通过极限的方式来求解。根据导数的定义，tanx在某一点x处的导数为lim(h→0) [tan(x+h) - tanx] / h。
三、tanx的导数计算过程
将tan(x+h)展开，可得tan(x+h) = (tanx + tanh) / (1 - tanx * tanh)。代入导数的定义式中，可以得到lim(h→0) [(tanx + tanh) / (1 - tanx * tanh) - tanx] / h。接下来，可以简化这个极限表达式。
四、使用泰勒级数展开式计算tanx的导数
除了使用极限计算导数，还可以使用泰勒级数展开法来求解tanx的导数。泰勒级数展开是一种将函数用无穷级数表示的方法，可以用来近似计算函数的值。
五、tanx的导数的特点
tanx的导数有一些特点值得注意。tanx在x=kπ+π/2（其中k为整数）处的导数不存在，因为tanx在这些点上的值为无穷大。tanx在x=kπ（其中k为整数）处的导数为0，因为tanx在这些点上的值为0。另外，tanx的导数是一个周期函数，周期为π。
六、tanx的应用领域
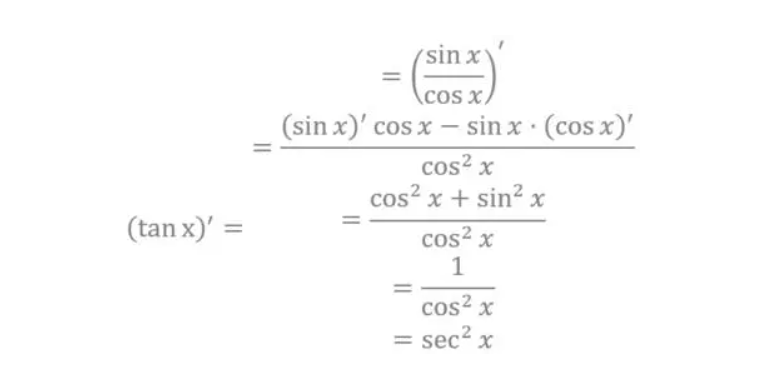
tanx在数学和应用中有广泛的应用。在三角学中，tanx常用于解决三角函数的相关问题。在物理学和工程学中，tanx常用于描述物体的斜度、电路中的电流等。tanx还在图形学、信号处理等领域中得到广泛的应用。
小结：
tanx是三角函数中一种常见的函数，其导数具有一定的特点。通过极限计算或者泰勒级数展开法都可以求解tanx的导数。tanx的导数在特定的点上不存在，有些点上为0。tanx在数学和应用中有广泛的应用领域。
