极坐标和直角坐标是数学中常见的坐标系统，在不同的数学领域和物理学中起着重要的作用。极坐标可以用一个点到原点的距离和与正半轴的夹角来表示，而直角坐标则是用一个点在x轴和y轴上的直角投影来表示。这两种坐标系统之间的转换公式可以帮助我们在不同的问题中应用正确的坐标系统。
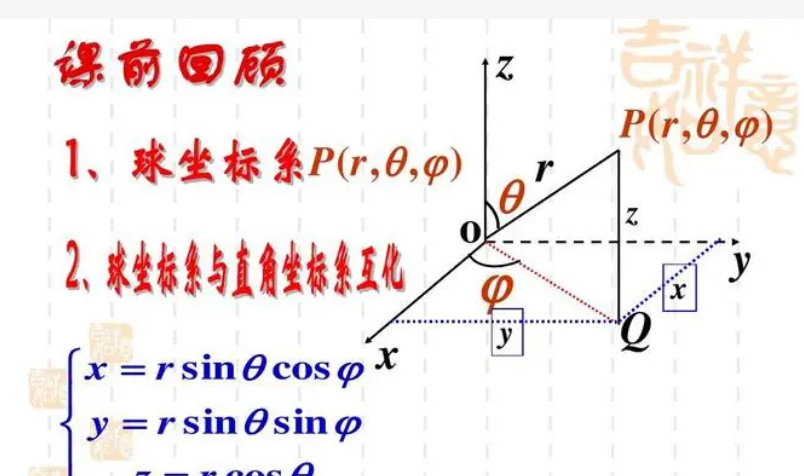
1. 极坐标转换直角坐标的公式是我们从极坐标系中将一个点的坐标转换为直角坐标系中的坐标。这个公式是由三角学和几何学的基本原理推导而来的。
2. 在极坐标系中，一个点的坐标可以用(r, θ)来表示，其中r是点到原点的距离，θ是点与正半轴的夹角。直角坐标系中的坐标用(x, y)来表示，其中x是点在x轴上的坐标，y是点在y轴上的坐标。
3. 要将一个极坐标点(r, θ)转换为直角坐标点(x, y)，我们可以使用如下的公式：
x = r * cos(θ)
y = r * sin(θ)
其中，cos(θ)表示夹角θ的余弦值，sin(θ)表示夹角θ的正弦值。
4. 这个公式的推导是基于直角三角形的几何关系。我们可以将极坐标点(r, θ)与直角三角形的边长和角度联系起来，进而得到以上的转换公式。
5. 在转换过程中，我们需要注意夹角θ的单位。通常，角度单位是度数，但是在数学计算中，弧度制更方便和常用。所以，在应用转换公式时，我们要确保使用正确的单位。
6. 有时候，我们也可以将直角坐标转换为极坐标。这个转换的公式是：
r = √(x^2 + y^2)
θ = arctan(y/x)
其中，arctan(y/x)是x轴到点(x, y)和原点形成的角的反正切值。
7. 极坐标转换直角坐标的公式在很多领域中有广泛的应用，尤其是在几何学、物理学和工程学中。例如，在计算机图形学中，我们可以使用这个公式将极坐标的图形转换为直角坐标的图形。
8. 这个公式也可以用于求解极坐标系下的各种问题，例如计算圆的面积、计算圆锥形的体积等。
结尾：
通过极坐标转换直角坐标的公式，我们可以在解决各种问题时，到合适的坐标系统，从而简化计算和求解的过程。这个公式的应用不仅局限于数学和物理学领域，还可以扩展应用于其他学科和实际问题的解决中。因此，了解和掌握这个公式对我们的学习和工作都具有重要的意义。
