dr在数学上什么意思

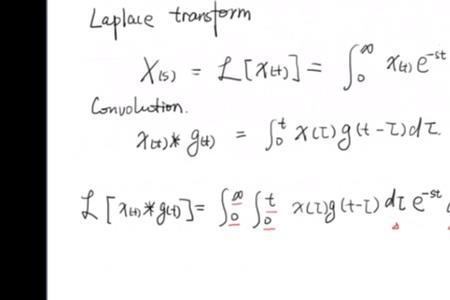
dr是r的微分

从数学上来说，导数dr/dt的定义就是 dr/dt=lim(△t趋向0时)△r/△t， 用文字来描述就是：r对时间t的导数，就是△r/△t当时间趋于零时的极限，也就是说，导数本来就是这样定义的

与物理不一样的是，数学上，r可以是任何函数，而大学物理中，一般用r（矢量）表示质点的位置函数。

dr在数学上什么意思

dr是r的微分（几何理解：微分就是切线方向增量）

4rdr就是4r和dr的乘积

∫4rdr其实把所有4rdr极限化的累加起来（参加积分的定义：将函数分段累加然后求极限）

从理解意义上说：积分符号∫就是求和Sum的极限化，因为求和是离散的，而积分是连续的，二者的转变就通过极限——将分段△r极限化最小为微元dr