RC振荡电路是一种基本的电路结构，广泛应用于各种电子设备中。在RC振荡电路中，由于电容器和电阻器的组合，会引发电路的振荡现象。本文将详细介绍RC振荡电路的频率计算公式的推导过程。
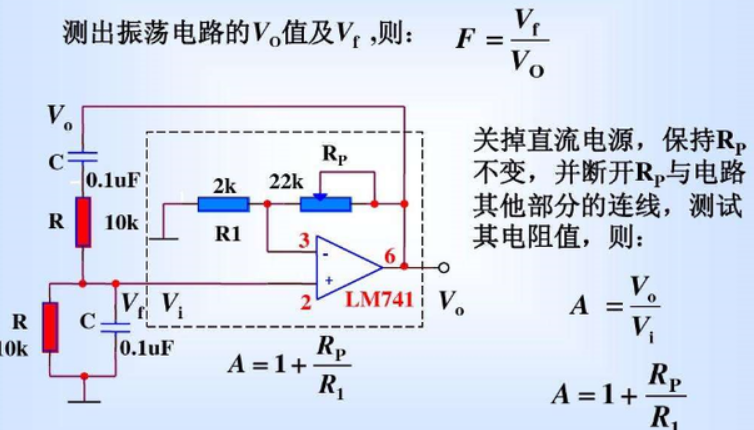
1. RC振荡电路的工作原理
RC振荡电路是由电容器和电阻器组成的串联电路。当电路中施加外加电源时，电容器开始充电，电荷通过电阻器逐渐放电。当电容器充电至一定程度时，电荷通过电阻器的速度与在电容器中的充电速度相等，此时电路中的电流和电压达到峰值。随着电容器电量的不断减少，电路中的电流和电压也会逐渐降低，直至下一个周期开始。
2. 推导RC振荡电路的频率计算公式
在RC振荡电路中，频率是指电路中振荡的周期数。频率计算公式为：
f = 1 / (2πRC)
其中，f表示电路的频率，R为电阻器的电阻值，C为电容器的电容量。
我们需要从振荡电路的工作原理出发，推导出振荡周期的基本公式：
振荡周期T = 2πRC
3. 推导过程
我们假设电路中的电压为V，电流为I。根据欧姆定律和电容器的电流公式，可以得到以下两个关系式：
V = IR (1)
I = C * dV/dt (2)
其中，dV/dt表示电压关于时间的变化率。
将式(2)代入式(1)中，可以得到：
V = RC * dV/dt
为了将上述微分方程简化，我们引入一个新的变量x，定义如下：
x = V / RC
将新定义的变量x代入上述微分方程中，可以得到：
x = dx/dt
对上述微分方程进行移项和积分，可以得到：
∫(dx/x) = ∫(dt/RC)
通过积分，可以得到：
ln|x| = (t + C1) / RC
其中，C1为常数。接下来，我们对上式取指数，可以得到：
x = e^((t + C1) / RC)
我们知道，在振荡过程中，电容器充电时电压逐渐升高，放电时电压逐渐降低。因此，我们可以令e^C1 = A，其中A为常数。
经过推导，我们可以得到振荡电路的电压公式如下：
V = A * e^(t / RC)
为了计算振荡电路的频率，我们需要找到电压的周期性变化。当电压变化一周期时，t的变化为T，因此我们将上述公式中的t替换为T，可以得到：
V = A * e^(T / RC)
另一方面，我们知道指数函数的周期为2π。因此，我们可以得到：
e^(T / RC) = e^(2π)
将上述公式整理，可以得到：
T = 2πRC
总结：我们推导出了RC振荡电路的频率计算公式：
f = 1 / (2πRC)
结论：
通过推导，我们得出RC振荡电路的频率计算公式为f = 1 / (2πRC)。通过这个公式，我们可以在设计和调试电子设备时准确计算RC振荡电路的频率，进一步提高电路的性能和稳定性。
